BooN basic features

See https://franck-delaplace.github.io/BooN/ for documentation.

import matplotlib.pyplot as plt
import networkx as nx
from tabulate import tabulate
from boon import *
from boon.logic import *

Boolean network definition

from sympy.abc import w, x, y, z, v
boon = BooN({x: y, y: x & z, z: w | ~x & v | y, w: x & y | ~x & z & ~w & ~v, v: ~v & w})

Variables of BooN:

print(boon.variables)

{x, v, w, y, z}

Print styles

Logical (default):

print(boon)

x = y
v = w ∧ ¬v
w = (x ∧ y) ∨ (z ∧ ¬v ∧ ¬w ∧ ¬x)
y = x ∧ z
z = w ∨ y ∨ (v ∧ ¬x)

Sympy:

boon.style = SYMPY
print(boon)

x = y
v = w & ~v
w = (x & y) | (z & ~v & ~w & ~x)
y = x & z
z = w | y | (v & ~x)

Mathematica:

boon.style = MATHEMATICA
print(boon)

x = y
v = w && !v
w = (x && y) || (z && !v && !w && !x)
y = x && z
z = w || y || (v && !x)

# Default style is LOGICAL
boon.style = LOGICAL

Delete v

boon.delete(v)
print(boon)

z = w ∨ y ∨ ¬x
w = (x ∧ y) ∨ (z ∧ ¬w ∧ ¬x)
y = x ∧ z
x = y

Renaming

Rename w to v

boon.rename(w, v)
print(boon)

z = v ∨ y ∨ ¬x
v = (x ∧ y) ∨ (z ∧ ¬v ∧ ¬x)
y = x ∧ z
x = y

Stable states

stable = boon.stable_states
tabulate(stable, headers='keys', tablefmt="html")

z	v	y	x
True	True	True	True

Stability constraints in logic:

prettyform(boon.stability_constraints())

'(x ⇔ y) ∧ (y ⇔ (x ∧ z)) ∧ (z ⇔ (v ∨ y ∨ ¬x)) ∧ (v ⇔ ((x ∧ y) ∨ (z ∧ ¬v ∧ ¬x)))'

Dynamics

Asynchronous model

# Define the datamodel of dynamics
M = boon.model()
# initialize figures
_, ax2 = plt.subplots()
ax2.axis('off')
boon.draw_model(M, pos=hypercube_layout(4), ax=ax2)

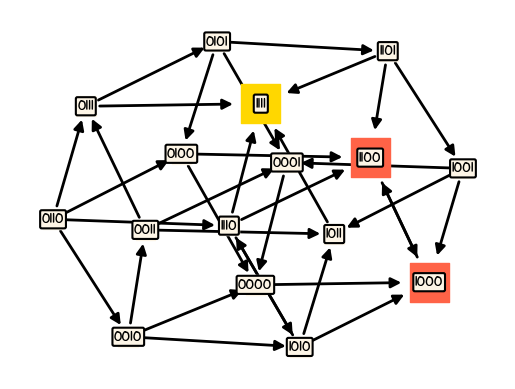
Synchronous model

# Synchronous datamodel
MS = boon.model(mode=synchronous, self_loop=True)
_, ax3 = plt.subplots()
ax3.axis('off')
boon.draw_model(MS, pos=nx.shell_layout(MS), ax=ax3)

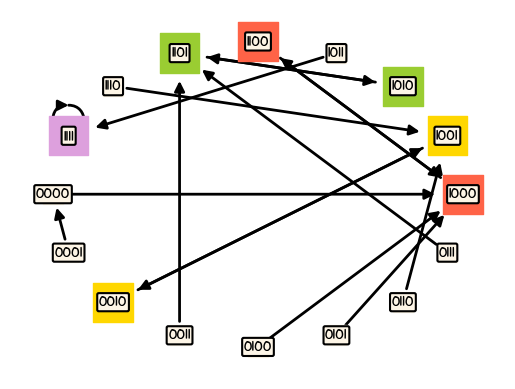
Equilibria

eqs = boon.equilibria(model=MS)
for eq in eqs:
    print(tabulate(eq, headers='keys'))

z     v      y      x
----  -----  -----  -----
True  False  False  False
True  True   False  False
z      v      y      x
-----  -----  -----  -----
True   False  False  True
False  False  True   False
z     v      y      x
----  -----  -----  -----
True  False  True   False
True  True   False  True
z     v     y     x
----  ----  ----  ----
True  True  True  True

Interaction graph

IG = boon.interaction_graph

boon.pos = nx.circular_layout(IG)
_, ax1 = plt.subplots()
ax1.axis('off')
boon.draw_IG(IG, modular=True, ax=ax1)

<networkx.classes.digraph.DiGraph at 0x7f1903ebd8d0>

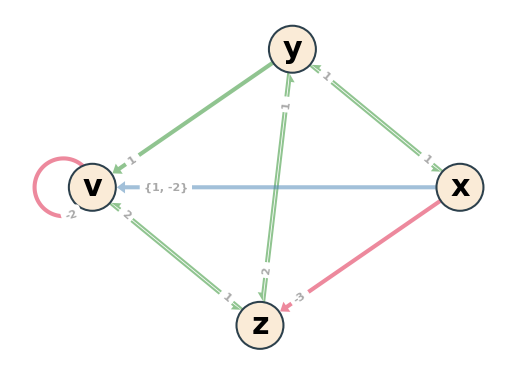
Retrieve BooN from the interaction graph

boon.from_ig(IG)
print(boon)

z = v ∨ y ∨ ¬x
v = (x ∧ y) ∨ (z ∧ ¬v ∧ ¬x)
y = x ∧ z
x = y

Save and re-load

boon.save("bn")
boon2 = BooN.load("bn")
print(boon2)

z = v ∨ y ∨ ¬x
v = (x ∧ y) ∨ (z ∧ ¬v ∧ ¬x)
y = x ∧ z
x = y

CNF conversion

boon2.cnf()
print(boon2)

z = v ∨ y ∨ ¬x
v = (x ∨ z) ∧ (x ∨ ¬v) ∧ (y ∨ ¬x)
y = x ∧ z
x = y

DNF conversion

boon2.dnf()
print(boon2)

z = v ∨ y ∨ ¬x
v = (x ∧ y) ∨ (z ∧ ¬v ∧ ¬x)
y = x ∧ z
x = y

Export and import from text file

boon2.to_textfile('boolnet')
boon2 = BooN.from_textfile('boolnet.txt')
print(boon2)

z = v ∨ y ∨ ¬x
v = (x ∧ y) ∨ (z ∧ ¬v ∧ ¬x)
y = x ∧ z
x = y

Import from GINsim, and compute stable states

import biolqm

This notebook has been executed using the docker image colomoto/colomoto-docker:2024-09-01

lqm = biolqm.load("http://ginsim.org/sites/default/files/Th_17.zginml")

Using local file Th_17.zginml

biolqm.save(lqm, "th17.bnet")

'th17.bnet'

b = BooN.from_textfile("th17.bnet")
print(b)

STAT6 = IL4R
Tbet_b2 = (STAT1_b1 ∧ STAT1_b2 ∧ Tbet_b1 ∧ ¬GATA3) ∨ (STAT1_b1 ∧ Tbet_b1 ∧ Tbet_b2 ∧ ¬STAT1_b2) ∨ (Tbet_b1 ∧ Tbet_b2 ∧ ¬GATA3 ∧ ¬STAT1_b1)
IL4 = GATA3 ∧ ¬STAT1_b1
IL12R = IL12 ∧ ¬STAT6
IFNbR = IFNb
IRAK = IL18R
SOCS1 = STAT1_b1 ∨ (Tbet_b1 ∧ ¬STAT1_b1)
IFNb = false
IFNg_b1 = (IFNg_b1 ∧ IFNg_b2) ∨ (Tbet_b1 ∧ ¬IFNg_b1) ∨ (IFNg_b1 ∧ Tbet_b1 ∧ ¬IFNg_b2) ∨ (STAT4 ∧ ¬IFNg_b1 ∧ ¬Tbet_b1) ∨ (IFNg_b1 ∧ STAT4 ∧ ¬IFNg_b2 ∧ ¬Tbet_b1)
IL18 = false
Tbet_b1 = (STAT1_b1 ∧ Tbet_b1 ∧ ¬STAT1_b2) ∨ (Tbet_b1 ∧ Tbet_b2 ∧ ¬STAT1_b1) ∨ (STAT1_b1 ∧ STAT1_b2 ∧ Tbet_b1 ∧ Tbet_b2) ∨ (STAT1_b1 ∧ STAT1_b2 ∧ ¬GATA3 ∧ ¬Tbet_b1) ∨ (STAT1_b1 ∧ ¬GATA3 ∧ ¬STAT1_b2 ∧ ¬Tbet_b1) ∨ (Tbet_b1 ∧ ¬GATA3 ∧ ¬STAT1_b1 ∧ ¬Tbet_b2) ∨ (STAT1_b1 ∧ STAT1_b2 ∧ Tbet_b1 ∧ ¬GATA3 ∧ ¬Tbet_b2)
STAT1_b2 = IFNgR_b1 ∧ IFNgR_b2 ∧ STAT1_b1
IL4R = IL4 ∧ ¬SOCS1
GATA3 = STAT6 ∧ ¬Tbet_b1
IFNgR_b2 = IFNgR_b1 ∧ IFNg_b1 ∧ IFNg_b2 ∧ ¬SOCS1
IL12 = false
IFNgR_b1 = IFNg_b1 ∨ (IFNgR_b1 ∧ IFNgR_b2 ∧ ¬IFNg_b1)
STAT4 = IL12R ∧ ¬GATA3
STAT1_b1 = IFNgR_b1 ∨ (STAT1_b1 ∧ STAT1_b2 ∧ ¬IFNgR_b1) ∨ (IFNbR ∧ ¬IFNgR_b1 ∧ ¬STAT1_b1) ∨ (IFNbR ∧ STAT1_b1 ∧ ¬IFNgR_b1 ∧ ¬STAT1_b2)
IL18R = IL18 ∧ ¬STAT6
IFNg_b2 = (IFNg_b1 ∧ Tbet_b1 ∧ Tbet_b2) ∨ (IFNg_b1 ∧ IRAK ∧ STAT4 ∧ ¬Tbet_b1) ∨ (IFNg_b1 ∧ IRAK ∧ STAT4 ∧ Tbet_b1 ∧ ¬Tbet_b2)

stable = b.stable_states
tabulate(stable, headers='keys', tablefmt="html")

Tbet_b1	GATA3	IL4	IFNg_b1	IFNg_b2	IFNbR	Tbet_b2	IRAK	IFNb	STAT1_b2	IFNgR_b2	IL12	IL4R	IL12R	SOCS1	IFNgR_b1	STAT4	IL18	STAT6	STAT1_b1	IL18R
False	True	True	False	False	False	False	False	False	False	False	False	True	False	False	False	False	False	True	False	False
False	False	False	False	False	False	False	False	False	False	False	False	False	False	False	False	False	False	False	False	False
True	False	False	True	False	False	False	False	False	False	False	False	False	False	True	True	False	False	False	True	False
True	False	False	True	True	False	True	False	False	False	False	False	False	False	True	True	False	False	False	True	False